Estudo de matemática para a física

Tanto em olimpíadas quanto nos próprios folhetos do curso de física, se torna claro que é necessário saber matemática para resolver questões, e isso não vai só na parte de fazer contas, mas sim na parte de usar álgebra vetorial, calculo, geometria (muito mais do que eu gostaria) para provas leis ou descrever um fenômeno. Isso não quer dizer que se eu ler um livro de física sem ter feito 50000 de exercícios de matemática eu não conseguirei entender nada, mas se torna claro como ter mais domínio sobre esses assuntos mencionados ajuda muito.

É com isso em mente que eu venho fazer esse post: Para o nível intermediário e avançado(Para pessoas que estão mais focados à estudar para a OBF, é deixado mais claro o que é útil desse post no Guia de Estudos), é necessário um bom domínio de matemática e, embora estamos planejando listas e simulados sobre o assunto, seriamos incapazes de explicar toda essa abrangente matéria. Para ajudar, então, eu coloquei aqui o que eu acho essencial ter domínio quando estudando física e onde daria pra estudar eles.

(por essencial eu digo daquilo que, sem estudar, fica extremamente complicado ver muitas coisas sobre. Só que é importante lembrar que existem assuntos que eu não menciono aqui porque tende a ser estudado junto com o assunto físico, então eu não vejo muito como essencial)

Como você pode ver, o post esta muito grande, e não quero dar a ideia você precisa ter estudado uma tonelada de assuntos matematicos antes de começar a estudar física efetivamente. Eu acredito que ambos devem andar em conjunto: estudando física sem muito domínio matemático vai gerar uma dificuldade em alguma questão, e é quando isso acontecer que a pessoa deveria estudar o suficiente até não ter mais essa dificuldade. É nesse sentido que o post deveria ajudar: eu deixo aqui recomendações para quando você se interessar em estudar essas coisas.

Lembrando também que tudo isso se trata apenas do meu ponto de vista, não quer dizer que eu sei tudo que precisa ser estudado, se você tem alguma recomendação melhor ou um ponto de vista diferente, sinta-se livre pra me contatar.

(Obs: depois de 5 horas escrevendo isso aqui, você pode perceber que, a medida que você chega mais embaixo no post, mais eu começo a ficar menos preocupado em fazer adendos e dar muitas explicações. Isso se deve ao fato da minha capacidade mental ser lentamente drenada a cada linha que eu escrevo, peço perdão.)

Matemática segundo o Syllabus da IPhO

No Syllabus da IPhO, é dito que para a prova é necessário o conhecimento matemático de:

1. Álgebra
2. Funções
3. Geometria
4. Vetores
5. Números Complexos
6. Cálculo
7. Estatística
8. Métodos aproximados e numéricos

Recomendo ver o Syllabus em si para se ter uma ideia melhor de o que ele se refere em cada coisa, mas também não se restrinja à somente o que está escrito ai: a ideia do Syllabus é dar uma visão geral do que esperar, mas as provas tendem a cobrar coisas além do que esta ai.

Com isso em mente, eu vou fala um pouco de cada um, o que eu recomendo para estudar, onde eu recomendo e onde eu já vi questões que usaram bastante disso.

Álgebra e funções:

Nesse caso em especifico Algebra em si aparece em tudo: Saber resolver equações de primeiro ou segundo grau; conhecer funções senoidais, círculos trigonométricos, relações de soma e subtração em funções senoidais, funções hiperbólicas; entender equações polinomiais, exponenciais ou logarítmicas, progressão geométrica e aritmética e o resultado de suas somatórias; ser capaz de escolher respostas com sentidos físicos; saber resolver sistemas de equações e fazer divisão de polinomios; entender análise combinatória(apesar que isso esta mais ligado na parte de estatística do que álgebra), matrizes, auto vetores, autovalores, determinante, entre outros. Tudo isso é importante pra caramba. Não é também como se toda questão que apareça por ai você terá que usar tudo isso de uma vez, mas sempre vai ter uma questão ou outra que vai ser necessário usar algo do tipo.

Pra aprender o básico de funções, como elas funcionam, como resolve elas, eu recomendo bastante as vídeo aulas do professor Ferreto, as aulas que ele fez há uns 4 anos atrás eram bem centradas nesses assuntos e ajudam muito. Canal do Professor Ferreto

Também recomendo o canal “Matemática Rio” pelos mesmos motivos, ele possui bastante aulas relacionadas com equações, funções e resolução de equações. Canal do Matemática Rio

Outro canal que eu recomendo é o “Responde Ai”, eles tentam tratar de assuntos mais avançados, assim como uma ótima introdução pra certos tópicos da física. Canal do Responde Ai

Pra minha ultima recomendação de canais pro estudo de álgebra, tem o canal “Blackpenredpen”. Eu nunca vi nenhum video onde ele busca esninar algum topico em especifico, mas ele resolve questões intrigantes e faz um uso grande de matematica, limites, derivadas, e outros que podem ajudar bastante a compreender mais da fisica. Canal Blackpenredpen

Algumas pessoas também mencionam para canal pra ver matemática sendo: BriTheMathGuy

Acho que esses são bons canais pra se ter uma boa ideia de que tipo de matemática se espera em olimpíadas(embora algumas coisas tratadas nesses últimos dois canais vão muuuuito longe do necessário).

Também convém avisar que cada um desses assuntos que eu mencionei já são uma ótima base para o que esperar em questões, e mesmo que os canais não falem deles, com certeza tem vídeos no youtube falando de cada um deles com detalhe. Ademais, muitos livros que vão falar desse assuntos que usem isso e eles não são tão triviais, o livro costuma introduzir à sua maneira esse tópico e seu desenvolvimento(num nível mais para seletiva mesmo). A exemplo disso, o Blundell tem um dos seus primeiros módulos dedicados especialmente à analise estatística e combinatória.

A minha maior dica é, no começo dos estudos da física pra seletiva, vê vídeos sobre assuntos matemáticos sem muita preocupação se vai ser importante ou não, para se obter um repertório próprio; ao mesmo tempo, à medida que algum recurso de álgebra aparece em algum tópico na física, seja em uma explicação ou numa questão, para um tempo pra pesquisar na internet e tentar entender bem esse recurso.
Pra fazer questões desses assuntos, recomendo tanto questões de matemática de vestibulares difíceis como o ITA e IME, quanto listas de exercícios de faculdades sobre esses assuntos:

• UFABC- Bases Matemáticas
• UFABC- Álgebra Linear (Algebra linear tem bastante relação tanto com matrizes quanto com geometria, tanto que algumas vezes a matéria é dada como: "Álgebra linear e Geometria Analítica". Alguns tópicos podem não ser tão relevantes à física, então fica aqui a dica que esse vale a pena ver antes o quão útil realmente é à suas necessidades)
• IME USP- Bases Matemáticas (Esse em especifico tem questão de muitos assuntos, incluso álgebra e funções, então eu colocarei esse dado em vários outros tópicos)

Como ultima recomendação, tanto para vídeos quanto para exercícios, deixo aqui o site do POTI( Polos Olímpicos de Treinamento Intensivo) eles focam em assuntos da OBMEP, OBM e coisa do tipo, então será notado uma grande diferença entre as vídeo-aulas deles e as do Blackpenredpen: o POTI trabalha muito mais com a ideia de teoremas e princípios que usam da indução e do raciocínio logico, e tão muito mais ligados à treinamento para as olimpíadas de matemática, ja o Blackpenredpen tenta mais falar de assuntos de matematica para a faculdade, e não foca tanto em olimpiadas. O POTI não deixa de ser um bom recurso pra estudar, mas é improvável que boa parte do que visto ai será usado diretamente numa questão de física.

Geometria

Geometria é um assunto um pouco mais delicado: Tem uma parte mais simples do conteudo que uma boa quantidade de assuntos usa, como Eletrica, mecanica, e até termodinamica; no entenato, tem uma parte beem mais complicada que trabalha com conceitos mais fundamentais de geometria. Esse ultimo aparece principalmente em questões de orbitas ou de lançamentos, e o problema é que esse tipo de questão pode ser usado o quanto quiser de geometria, tudo depende do que é realmente útil para à questão e isso é impossível de ser previsto. (Não é a toa que eu tenho trauma de geometria em questões da Physics Cup)

Para lidar com esses problemas um por um, eu acredito que é importante primeiramente ter domínio dos tais assuntos mais simples e diretos: semelhança de triângulos, propriedades de triângulos, calculo de áreas de quadriláteros e figuras regulares, compreensão sobre figuras tridimensionais, volumes de certos poliedros, lei dos senos, lei dos cossenos, entre outros.(Nota que o "entre outros" é bem amplo. Geometria básica costuma ser algo tão aberto que eu nem consigo tentar me expandir muito sobre esse tópico)

Para estudá-los, videos de geometria do Professor Ferreto e do Matemática Rio me ajudaram bastante. O Site do POTI no quesito de geometria mais basica é muuuuuito bom(pelo menos foi pra mim) Acho que questões de matematica da OBMEP tendem a ser boas pra treinar esses assuntos.

Ademais, acredito que uma das coisas mais importantes de se entender sobre geometria, além do simples, é as definições geométricas e propriedades de uma parábola, de uma elipse, de um circulo e de uma hipérbole. Digo definições no plural porque é justamente isso que complica tanto questões: existem 300 trilhões de maneiras de descrever geometricamente uma curva e cada questão pode usar uma definição diferente.
Vou deixar aqui recomendações pra cada tipo de curva(sim, eu estou realmente dando recomendações de onde estudar cada curva, esse é o nível de abalo que essas coisas me dão).

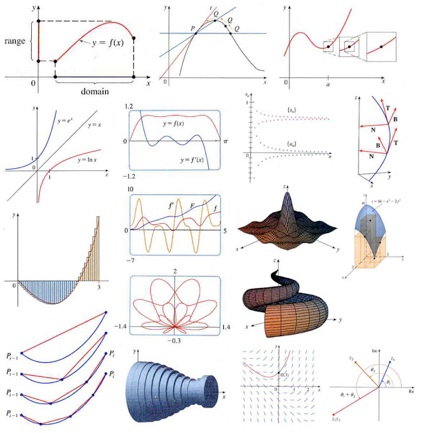
Parábolas

Vídeos do Khan Academy, Vídeo do Responde Ai Folheto de lançamento parabólico do Physoly, Boa e Velha Wikipédia (apesar que na Wikipédia ele tende a ser bem direto), e diversos outros que podem ser encontrados na internet quando procurado sobre, nesse mesmo contexto tem o nosso folheto de Conicas e Orbitas, o qual na parte de parábolas se dedica a explicar matematicamente o que ela é . O lugar onde mais é encontrado parábolas é em lançamentos parabólicos na terra e para a orbita de um planeta quando a sua energia é zero( o qual é uma parábola), há questões de mecânica que usam da definição de parábola por foco e diretriz pra achar a trajetória de uma partícula. Outra utilização que eu conheço é “Espelhos Parabólicos” que também usam a propriedade de Foco de Diretriz para provar o que acontece com raios de luz que chegam no espelho(Algo que se não me engano o folheto do Physoly fala sobre).

Elipses

Para elipses é um pouco menos direto, do que eu vi o melhor lugar para estudar sobre é na Wikipédia (se você conhecer outro lugar e tiver outra recomendação, aceito muito), deixo também de recomendação o nosso folheto de Cônicas e Orbitas, no qual o começo é uma introdução à geometria. Do que eu vi por ai nos últimos anos, o mais essencial de se saber de uma elipse é: definição geométrica pelos dois focos, saber o que é a excentricidade qualitativamente e matematicamente, semieixo maior, semieixo menor, saber a área de uma elipse, saber as definições de Afélio e Periélio, saber a definição matemática de uma elipse, tanto em coordenadas cartesianas quanto em coordenadas polares. Nos folhetos de gravitação do curso de física, foi feito bastante uso das propriedades geométricas de uma elipse para desenvolver as formulas usadas, e é basicamente nisso que o maior conhecimento de elipse se torna necessário. Outro caso em que elipse é comum é em polarização de ondas: Oscilações harmônicas perpendiculares com a mesma frequência mas com diferentes fases tem como forma geral uma elipse, e para provar isso é necessário ter conhecimento da descrição matemática de uma elipse rotacionada (não que eu entenda isso totalmente, mas é no mínimo interessante saber um pouco disso). Em gravitação existe o conceito de “Elipse de segurança” que usa bastante das propriedades geométricas de uma elipse também. Uma ultima propriedade conhecida de elipses é o espelho de elipsoide (mas isso é raramente mencionado), que usa as propriedades angulares de uma elipse.

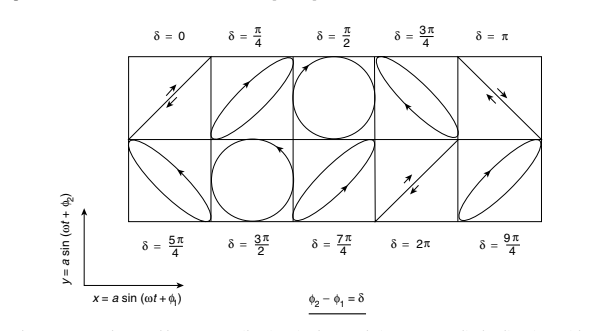
Círculos

Círculos é um pouco complicado achar algum lugar onde realmente é falado de cada propriedade que pode ser usada (porque teoricamente existem infinitas propriedades, a questão é o quanto você realmente usa delas), acredito que os dois melhores lugares que eu achei pra ver algo sobre círculos é a Wikipédia e um Condensado de propriedades geométricas de um circulo feito pelo Brilliant. Círculos não possui um limite de onde é pedido e como é pedido, existem varias questões que tem alguma propriedade que podem ser resolvidos pela introdução de um circulo. Acredito eu que as propriedades mais importantes usadas em questões é o teorema de Tales, o teorema do ângulo central ser o dobro do ângulo na circunferência e o teorema da reta tangente.

Hipérbole

Hipérbole é como se fosse o filho ignorado das orbitas: ele é o menos falado das cônicas, e acho que o melhor jeito de ver algo sobre é no folheto de Cônicas e Orbitas e Wikipédia. Eu só vi ela sendo usada em Orbitas e em relatividade (porque um movimento é descrito num gráfico por uma hipérbole), então ela não é tãaaao importante assim, mas mesmo assim um conhecimento para orbitas é necessária, principalmente sua descrição matemática em coordenadas polares, apesar que quando os livros costumam introduzir propriamente essa parte.

Vetores e álgebra linear

Vetores e Álgebra linear estão intimamente relacionados, e estudar um muitas vezes diz respeito a estar estudando o outro. O conceito de vetores pode ser usado amplamente em questões de física, sendo muitas vezes um recurso “geométrico” que pode resolver muito mais facilmente as questões do que se tentado resolver puramente usando números. Vetores tem uma interpretação que parte muito mais para a geometria e tem umas que vão muito mais para uma descrição puramente matemática( que é onde a álgebra linear mais foca, mas não é uma regra geral), e infelizmente é necessário saber as duas maneiras com boa precisão. É importante demarcar que vetores é algo que eu vejo como um assunto essencial para estudar física: alguns livros vão introduzir mas também não vão se dedicar tanto a fazer uma explicação bem feita de o que é, suas transformações e como pode ser usado, então eu recomendarei aqui exercícios e vídeos para aqueles que sabem muito pouco de vetores e suas transformações ou buscam só revisar algo, mas creio que não estarei dando um repertório absurdo pra resolver questões com facilidade absurda.

O assunto de álgebra linear é bem comum quando é sobre vetores, mas fora isso ele é um pouco mais raro de ser visto, acredito que a segunda maior utilidade é em “Auto vetores e Autovalores”.

Para estudar Vetores, Produto Vetorial e Produto escalar, eu recomendo o vídeo de vetores da playlist Universo Mecânico, a playlist do Responde Ai, e o vídeo de qualidade questionável de Eugene Khutoryansky para se ter uma introdução sobre álgebra linear com vetores, recomendo Playlist do canal “3Blue1Brown” (Importante destacar que alguns vídeos fazem muito uso de matrizes, então se não há muito domínio com ele, ou é melhor estudar um pouco ou aceita que as coisas vão parecer um pouco jogadas)

Para fazer questões sobre o essencial de Vetores, recomendo as listas de exercício da UFABC de geometria analítica e a lista de geometria analítica do Baver.

Outras listas podem ser feitas, exercícios de vetores do Moyses 1 também são relativamente bons, mas sendo a minha intenção dar algo para que as pessoas possam se familiarizar com o assunto, creio que com o que esta aqui, é o suficiente. Exercícios de Algelin eu não tenho muitas recomendações, parte porque eu sinto desnecessário: quando álgebra linear é introduzida no conceito de auto vetores e autovalores, os livros tendem a evitar o máximo de usar muitos conceitos avançados, então saber o básico por vídeo já deve ajudar muito.

Números Complexos

O conhecimento necessário de números complexos é relativamente curto: É necessário entender o que seria um numero imaginário, a representação geométrica de um numero complexo, quando um numero complexo aparece, operações simples com ele e exponenciais complexas (que é sem duvidas o mais importante nesse assunto para a física). Alguns livros tendem a explicar boa parte desses assuntos, e nisso muitas vezes estudar muito não é necessário( Deixo aqui minha recomendação ao livro A.P. French Vibrations and Waves, ondulatória é uma das matérias que mais usa de números complexos, e esse livro faz uma explicação muito boa e racional de o que são e como usar, apesar que ela tende a usar um pouco de calculo também), porém, a ideia de numero imaginário é muitas vezes não trivial no começo, e ver isso previamente pode facilitar eventuais problemas. Sobre o quesito de exponenciais complexas, eu creio que seja um pouco mais complicado de começo entende-las sem ter visto um pouco de calculo antes: a maioria das provas de exponenciais complexas utiliza ou do conceito de equação diferencial ordinária e as derivadas de seno e cosseno, ou do conceito de Serie de Taylor e derivadas de exponencial, seno e cosseno, e então é necessário pelo menos ter visto um pouco de cada pra não quebrar incrivelmente.
Exercícios sobre números complexos eu acho bem desnecessário, eu deixo aqui então apenas recomendações para se ter familiaridade com essas quantias:
Para ter uma introdução pra quem nunca viu números complexos, recomendo o vídeo do Eddie Woo, que não tenta ir tanto para contas, mas sim explicar o que seria números complexos.
Sabendo o que é um numero complexo, recomendo o Vídeo do 3Blue1Brown de números complexos que mostra como ele pode ser usado para fazer contas, como fazer distinções etc. Também recomendo vídeos do Blackpenredpen, onde tem alguns que são dedicados unicamente a resolver questões interessantes envolvendo números complexos( o terceiro vídeo mais visto dele por exemplo).
Exponenciais complexas, formula de Euler e coisas do tipo eu creio que vale mais a pena esperar para ver em um livro já tendo o repertório necessário para tal.

Cálculo

O Cálculo é sem duvida um dos recursos matemáticos mais necessários para se ver física no quesito de olimpíadas internacionais: muitos livros podem não usar de calculo para desenvolver algum tópico, visto que nem tudo precisa de uma derivada ou uma integral, mas quando ele precisa, o livro nem se preocupa em tentar explicar calculo, e o conceito é tão abrangente que tentar ler algum livro difícil sem ter visto calculo dá uma sensação de que há uma ponte gigante de conhecimento entre o que você sabe e o que é necessario para entender o livro. A ordem padrão que eu conheço de como se aprende calculo é:
Aprende limites, aprende derivada, aprende regra de derivadas e derivadas mais simples e mais comuns junto com sua notação na física, entende o conceito de máximos e mínimos, aprende o conceito de integrais, regras de integrais e integrais mais simples, aprende serie de Taylor, aprende equação diferencial e como resolve e depois derivadas vetoriais(Gradiente, divergente e rotacional).
Esse eu acho que é o mais essencial que alguém precisa ter estudado antes de tentar estudar muita física: livros como Morin, Purcell, Blundell, Griffiths, A.P. French, etc (que eu reconheço como sendo os livros base para se estudar fisica, mas é mais uma opinião própria do que um fato consumado). Assume que seus leitores possuem conhecimento sobre o básico de calculo (alguns até bem mais que o básico) e creio ser bem difícil tentar aprende-lo apenas lendo esses livros. Deixo aqui primeiramente o quanto cada livro que eu falei aqui espera que você saiba de cada assunto, e o que ele ensina de maneira razoável:

• Morin – Exige a compreensão de derivadas, integrais, diferenciais e Série de Taylor. Ensina como resolver equações diferenciais ordinárias no módulo de oscilações(que é onde se costuma entender bem esse assunto, mas ver vídeos na internet sempre é bom) e em rotações tem um desenvolvimento muito bom para a compreensão de derivadas de vetores.
• Purcell – Exige o conhecimento de bastante integrais, derivadas, diferenciais e Série de Taylor, mas tem uma explicação muito boa de integral de linha e explica também o conceito de gradiente, divergente e rotacional.
• Griffiths – Um pouco análogo ao Purcell, porém o Griffiths possui dois módulos iniciais totalmente dedicados à explicação de calculo, derivadas vetoriais e integrais de linha, um bom jeito para se aprender sobre esses dois últimos também.
• Blundell – Exige conhecimento de integrais, derivadas, diferenciais e Série de Taylor, seus módulos dão um desenvolvimento gigante pra o uso de integrais pra probabilidade e calculo de quantias médias, os seus apêndices possuem uma quantia absurda de desenvolvimento matemático, principalmente para achar integrais “especiais”.
• A.P. French e livros de oscilações em sua maioria (Pain, Crawford, Hecht, etc.) – Exige conhecimento de derivadas, integrais, diferenciais, Série de Taylor e solução de equação diferencial ordinária, de calculo quase sempre é muito mais ensinado sobre como usa-la para resolver algo em especifico o que como ela funciona em geral.

Falamos agora sobre aprender calculo em si:

Limites

A primeira coisa é sem duvidas entender o que são limites, porque existem e como calcula eles. Para isso existem trilhares de vídeos no Youtube, e recomendo alguns aqui:
Noção intuitiva de Limites pelo Professor Ferreto, Introdução aos limites GRINGS e Limites 1 da UNIVESP. Esses 3 possuem uma playlist extensa sobre limites e calculo, e não é uma má ideia ver mais alguns videos deles para ver se entendeu bem.
Limites trabalham muito com propriedades matemáticas e são essenciais para o desenvolvimento de calculo diferencial, então fazer exercícios também é interessante para se treinar:
Exercícios de Bases Matemáticas UFABC (o qual possui duas listas de limites)
Listas de Calculo 1 da IME-USP: Lista 1 e Lista 2 (ambas são listas de calculo, então o seu começo é de limites mas no seu desenrolar as questões já vão para derivadas e integrais, fique de olho até que ponto vale a pena fazer alguma questão dai então)

Derivadas

Visto limites, é necessário entender o que seria derivadas, como elas funcionam, quais são as regras de derivação e as integrais mais importantes de se saber. Para isso, recomendo a playlist de derivadas do Ferreto, o Curso de derivadas do GRINGS, as aulas de derivada da UNIVESP e, como recomendação especial além dessas, o vídeo do universo mecânico de derivadas. Deixo aqui a minha recomendação ao vídeo do universo mecânico pois meu processo para entender o inicio de calculo foi: No começo do meu 1ºano, o grupo de física da minha escola quis dar 1 semana de aulas destinadas à explicação de calculo, e na segunda aula o professor explicou derivadas e recomendou esse vídeo; na aula eu não entendi absolutamente nada, mas, ao ver o video, minha mente transcendeu e as coisas ficaram bem mais racionais.

Visto vídeos que explicam bem o que seria calculo, as derivadas mais padrões e as regras de derivada, é essencial fazer exercícios para se ter um domínio relativamente bom. No entanto, as minhas recomendações para exercícios seriam as mesmas de antes, listas de faculdade de calculo, e acredito que seja possível encontra-las procurando no Google e por isso não vou repeti-las.

Integrais

Visto derivadas, junto com o conceito de máximos e mínimos, que é direto de derivadas, o caminho normal seria ver o que são integrais, como calcula-las, e quais regras precisam e podem ser usadas. Ppara isso eu recomendo: Aulas do “Responde Ai” de integrais, Aulas do GRINGS de integrais, Aulas de Integrais da UNIVESP e o Vídeo de integrais do Universo Mecânico. Outros vídeos podem ser encontrados na internet, e sinta-se livre pra procurar alguns você mesmo. Para exercícios, a dica é a mesma:
Exercícios de funções de uma variável da UFABC ( a partir da lista 7, tem questões de integrais, então é um bom jeito pra treinar)
Exercícios de integrais da UTFPR
E diversas outras listas de exercício de faculdades sobre esse assunto.

Série de Taylor

Visto integrais e tendo um domínio razoável do que ela é, suas regras e as integrais mais comuns, o próximo passo seria conhecer a Série de Taylor, e para isso eu não recomendo muitos exercícios pois seu uso não é tão abrangente, e questões de faculdade vão para um escopo muito além do necessário para física, ao meu ver. Para estudar Série de Taylor, eu recomendo: Playlist do Super exatas de Série de Taylor(que é curta mas bem direta para entender quase todo o necessário sobre o assunto) e Aulas da UNIVESP sobre Série de Taylor. Note que, com esses videos, se torna possível estudar um pouco mais sobre exponenciais complexas e seus usos na fisica, porém eu não vejo muito como um conhecimento essencial visto que livros de ondulatória costumam desenvolver bem essa parte dado o conhecimento de calculo.

Diferente dos outros assuntos que eram usados sem muitos contextos em diversas questões, Série de Taylor é usado quase sempre em questões de física quando aproximações precisam ser feitas para se descrever um fenômeno: ou aproximações de primeira ordem para se ter uma dependência linear entre termos(aparecendo sem muitas regras definidas, bem comum), ou uma expansão de segunda ordem para uma dependência linear na derivada desses termos (mais relacionado à aproximação de movimento harmônico ao redor do ponto de equilíbrio, mais ligado à oscilações).

Equações diferenciais

Visto Série de Taylor, o próximo passo seria entender e saber resolver Equações diferenciais, para isso eu não recomendo um vídeo ou listas de exercícios, mas sim questões do livro: Introduction to Classical Mechanics, David Morin (Lembrando que baixar PDF’s de livros na internet não é considerado um crime no Brasil), no modulo 3 é mostrado como calculo pode ser bem usado para resolver questões de mecânica, já no modulo 4 é desenvolvido mais diretamente um processo de como resolver equações diferenciais ordinárias e seu uso na física.

Visto Equações diferenciais, o mundo do calculo pra física já está quase totalmente tracejado pra seguir sem mais ter que explodir com limites e várzea, a única coisa que será introduzido de novo na física será o conceito de Gradiente, Divergente, Rotacional e Integral de linha, o qual é basicamente uma mistura de derivadas e vetores, junto com transformações vetoriais. Para estudar isso, eu novamente não recomendo vídeos ou listas de exercícios, mas sim o livro: Introduction to Eletrodynamics, David J. Griffiths, O seu modulo 1 é totalmente destinado à mostrar o essencial de calculo, vetores e etc. e em certo ponto ele introduz os conceitos mencionados acima, sendo ai onde eu e muitas outras pessoas foram introduzidas à esses tópicos.

Com isso, você esta quase fechado em calculo, pode dormir em paz sem quebrar com muitas coisas relacionadas à isso
Como ultima recomendação, deixo a curta Playlist de Calculo Diferencial do 3Blue1Brown, que da uma comprimida em quase tudo que foi mencionado ai.

Estatística

A estatística necessária para o estudo de física não é muito abrangente, e minhas recomendações são bem diretas:
Conhecer os conceitos de Média, Desvio Padrão, Moda e Mediana.

Conhecer e ter um domínio relativamente bom de análise combinatória e calculo probabilístico ( o que definitivamente é a tarefa mais complicada dessas mencionadas, análise combinatória é algo relativamente abrangente e as questões de física do assunto podem ir bem longe, só que à medida que a dificuldade aumenta, menor é a chance de algo do tipo aparecer). Um lugar bom que eu achei para o estudo de análise combinatória e probabilidade é na Playlist do Paulo Pereira (nota que não estou dizendo que você sai dessa playlist tendo análise combinatória no bolso, mas sim que alguém que não sabe nada sai dai sabendo bastante coisa).

Dito isso, boa parte do necessário de estatística na física é apresentado no modulo 3 do livro Concepts in Thermal Physics, Stephan J. Blundell and Katherine M. Blundell , então é lendo esse livro que você deve ter o primeiro contato com esse tipo de coisa e também deixa um pouco claro onde é esperado o maior uso de estatística na física: questões de termodinâmica (não é atoa que é nessa área que existe a tal “Mecânica Estatística”).

Métodos aproximados e numéricos

Chegamos então ao ultimo tópico do Syllabus da IPhO, e é nesse que eu falho: Nunca estudei Métodos aproximados e numéricos de maneira focada nesse assunto, então eu não sei dizer onde é o melhor lugar para se estudar e como se estudar. O Syllabus diz que esse assunto está relacionado também à saber linearizar usando Série de Taylor ( o qual já foi dito antes) e ao chamado “Perturbation Method”. Eu nunca estudei esse ultimo, então não sei o que ele deveria significar, no entanto há uma vídeo-aula do MIT sobre esse assunto, então deixo aqui então como minha recomendação para se estudar sobre essa área.

Com isso, creio ter abrangido todos os tópicos da matemática que é usado na física. É absurdo a quantidade que realmente deve ser estudado simplesmente para se conseguir resolver questões de física, porém eu relembro aqui que geralmente se estuda para a seletiva por 1 a 2 anos, então o tempo é relativamente grande para se naturalizar com esses assuntos e resolver bastante questões para se ter um bom domínio.